Ejemplos representación de funciones lógicas

Con lo aprendido anteriormente...

1) Dada la función: F(x ,y)= x.y + x´ , representarlas.

2) Dada la función: F (x , y )= (x.y)´

Para este ejercicio hay dos soluciones posibles, utilizar dos compuertas NOT y una AND o solamente una NAND.



3) Dada la función F(x , y , z)= z´.y + z.y + x´.y.z

FUNCIONES LÓGICAS

FUNCIÓN LÓGICA AND: 

-Esta es una función lógica que tiene la siguiente tabla de verdad:

Esta función es una MULTIPLICACIÓN F(A,B)= A.B, en esta tabla se ven reflejados todos los casos posibles que pueden aparecer.

¿que para si en la entrada tengo "n" variables?

Es muy sencillo viendo esta tabla de verdad. Solamente va a ser "1" cuando todas las variables tomen el valor lógico "1", en caso contrario, tomara el valor lógico "0".

FUNCIÓN LÓGICA: 

-Tabla de verdad:

Esta función lógica llamada OR es una suma especial, ya que solamente puede tomar dos valores posibles "0/1".

¿que para si en la entrada tengo "n" variables?

Solamente tenes que pensar en esto, si al menos una variable toma el valor lógico 1, en la salida, tomara el valor lógico "1".


FUNCIÓN LÓGICA NOT:

Tabla de verdad:

Esta función lógica es muy sencilla, solamente donde tengo "0" en la entrada en la salida voy a tener el valor contrario ("1").

FUNCIÓN LÓGICA NAND:

Tabla de verdad:

Esta función lógica es como la inversa de la AND, cuando en la función lógica AND vale "1", en la NAND vale "0" y viceversa. 

"Esta función se la denomina la función negadora de la AND".

FUNCIÓN LÓGICA NOR:

Tabla de verdad:

Esta es la función negadora de la OR, donde en la función lógica OR vale "1" en la NOR vale "0" y viceversa.

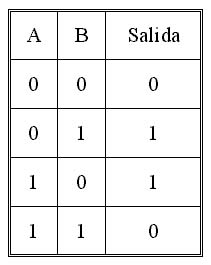
FUNCIÓN LÓGICA XOR:

Tabla de verdad:

Esta función lógica es la siguiente F(A,B): A´ . B +  A . B´  ,  donde " ´ " este símbolo significa la compuerta negadora NOT.

"Este blog esta echo por estudiantes para estudiantes", se agredecera cualquier acotación para mejor el contenido de este blog.

GRACIAS.-